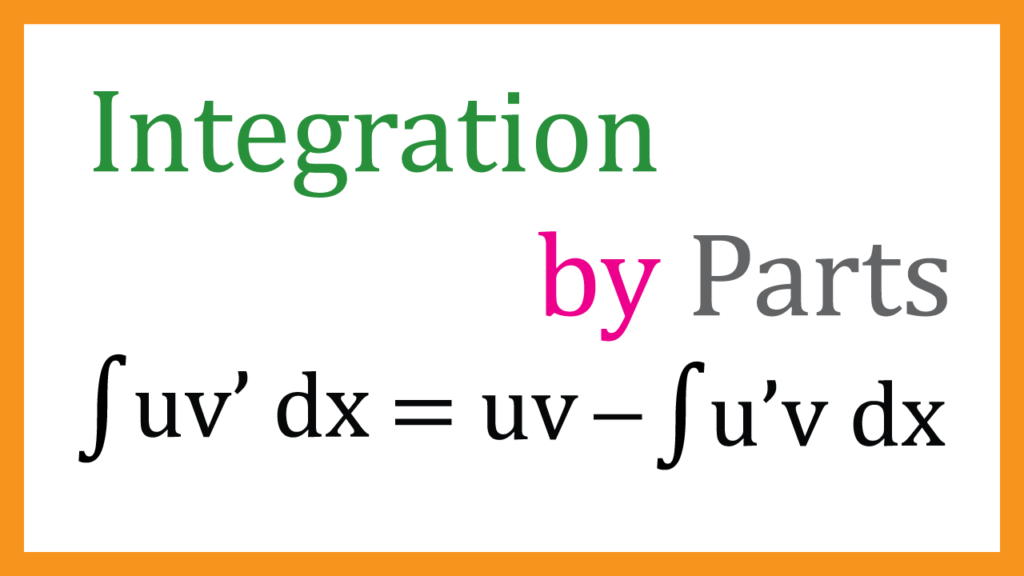
What is it
When there are 2 functions(composite function) in an integration operator, we can use the method, Integration by Parts.
It is used for combination of functions in an Integral. For examples, Polynomial functions(\(x,\ x^2,\ x^3, ・・・)\), Exponential functions\((e^x,\ 2^x, ・・・)\), Trigonometric functions\((\sin{x},\ \cos{x}, ・・・)\), Logarithmic functions\((\log{x},\ \ln{x})\) and so on.
This is one of most important formula for EJU Math. So let’s memorize it.
How to use
Example 1
$$\int x e^x dx$$
This is combination of a polynomial(\(x\)) and Exponential function (\(e^x\)).
We can use this formula to solve it.
$$\int u v’ dx=
u v
-\int u’ v’ dx $$
\(v’\) indicates the differentiation of \(v\). And please remember that I avoid writing like \(u(x)\) because \(u\) and \(v\) are obviously functions of \(x\).
We set
$$\color{blue}{u=x},\ v’=e^x$$
Now we have to find \(u’\) and \(v\)
$$\color{red}{u’=1},\ \color{purple}{v=e^x}$$
Then we substitute those values to appropriate places.
Since the formula is
$$\int u v’ dx=
\color{blue}{u} \color{purple}{v}
-\int \color{red}{u’} \color{purple}{v} \ dx $$
$$\int u v’ dx=
(\color{blue}{x}) (\color{purple}{e^x})
-\int (\color{red}{1}) (\color{purple}{e^x}) dx $$
$$=x e^x-e^x+C$$
$$=e^x(x-1)+C$$
Deviation for Integration by Parts
Let’s differentiate a composite function\(uv\)
Since it is a composite function, we need to use product rule for the differentiation.
$$(uv)’=uv’+u’v$$
Then we integrate for both sides
$$\int (uv)’ dx= \int uv’ dx + \int u’v \ dx$$
If we isolate the second term in the right side, \(\int uv’ dx\)
$$ \int uv’ dx = \int (uv)’ dx – \int u’v \ dx $$
Since \(\int (uv)’ dx = uv\), we eventually have
$$ \int uv’ dx = uv – \int u’v\ dx $$
This is the formula for Integration by Parts.
コメント