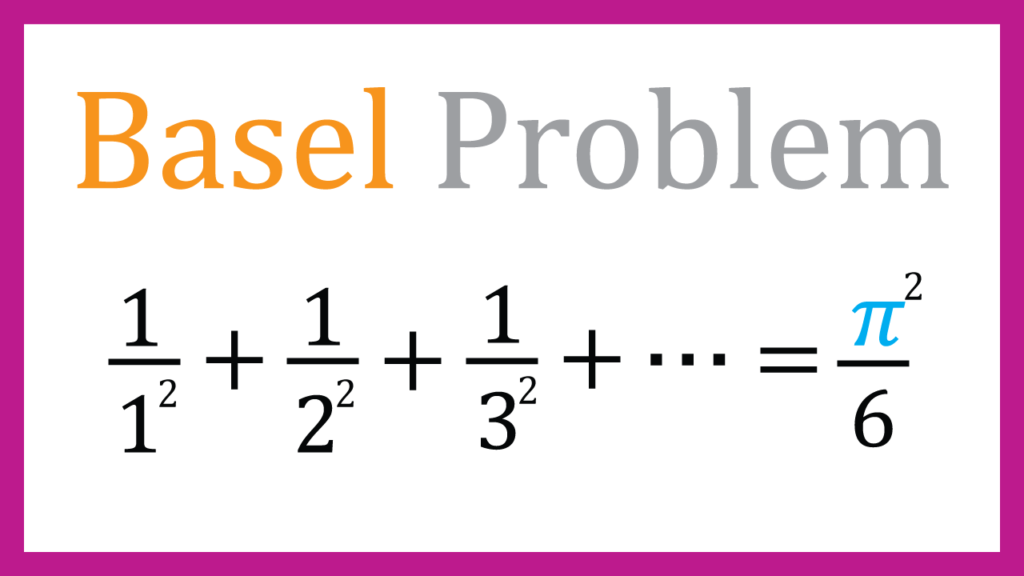
数学の有名な式にリーマン・ゼータ関数というものがあって
$$\zeta_{z}=\frac{1}{1^z}+\frac{1}{2^z}+\frac{1}{3^z}+\frac{1}{4^z}+・・・$$
というものだ。
これは素数に規則性があるかどうか検証するリーマン予想に関係する数式のようで、その中で\(z=2\)のとき、つまり
$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+・・・$$
と分母の指数が全部2となったとき、どうゆう結果になるのかという話である。
結果から先に言うと
$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+・・・=\frac{\pi^2}{6}$$
となる。
おいおい何で円に関係なさそうな数列に\(\pi\)が出てくるねん…と思うかもしれないけど、こういうことは結構よくあることのようだ。
意味はよくわからないけど、なんかロマンを感じるのは事実。
論理が導く不思議な現象を堪能したいと思う。
バーゼルの問題が2以下であることの証明
いきなりバーゼル問題が\(\frac{\pi^2}{6}\)であることを示す前に、まずこれが2以下になることを証明してみよう。実際、\(\frac{\pi^2}{6}=1.644934…\)である。
$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+・・・$$
これの各項をかけ算で表してやると
$$\frac{1}{1}\frac{1}{1}+\frac{1}{2}\frac{1}{2}+\frac{1}{3}\frac{1}{3}+\frac{1}{4}\frac{1}{4}+・・・$$
となる。そして、これより少しばかり大きい数列として
$$<\frac{1}{1}+\frac{1}{1}\frac{1}{2}+\frac{1}{2}\frac{1}{3}+\frac{1}{3}\frac{1}{4}+・・・$$
を用意する。これを思いついたのはすごいとしか言いようがないけども、それ自身の数列をいじるのではなくて、扱いやすい他の数列を比較対象と置くことで問題を解決しているのは、そのテクニックに美しさを感じる。
もちろん決して自分では思いつかないから、この論理的手法を美術作品のように鑑賞するのだ。
この並びの良いところは、かけ算で表された各項が引き算で書き換えられるところだ。どういうことかって?これを見てくれたまへ。
$$\frac{1}{1}\frac{1}{2}=\frac{1}{1}-\frac{1}{2}$$
$$\frac{1}{2}\frac{1}{3}=\frac{1}{2}-\frac{1}{3}$$
ほほう。これはおもしろいトリックだ。
どうやら分母のかけ合わす数字が連続しているときは、分母の小さいほうから分母の大きいほうを引くことで、同じ結果になるようだ。
これを使えば、かけ算の項がなくなり
$$\frac{1}{1}+\bigg(\frac{1}{1}-\frac{1}{2}\bigg)+\bigg(\frac{1}{2}-\frac{1}{3}\bigg)+\bigg(\frac{1}{3}-\frac{1}{4}\bigg)+・・・$$
かっこを取るとわかりやすいかもしれない
$$\frac{1}{1}+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+・・・$$
すると第3項以降が打ち消されるのがわかる。これは数列をやっていて一番気持ち良い時だ。この項を無限個まで増やしてやって、打ち消されるものを省けば
$$\frac{1}{1}+\frac{1}{1}-\frac{1}{\infty}$$
結局、\(\frac{1}{\infty}=0\)なので、バーゼル問題のもともとの数列より少しだけ大きいものとして新たに紹介された数列は
$$\frac{1}{1}+\frac{1}{1}\frac{1}{2}+\frac{1}{2}\frac{1}{3}+\frac{1}{3}\frac{1}{4}+・・・=2$$
ということになる。この数列は2に収束するのだ。ということはこれより小さいはずのバーゼルの問題は
$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+・・・<2$$
これがバーゼル問題の数列が2より小さい証明である。
バーゼル問題が\(\frac{\pi^2}{6}\)になる証明
数学の美しいトリックを堪能できたけれども、ここまで来たらキッチリとしてた結果を出してしまいたいところである。
今回は困ったときのテイラー展開を使う。\(sinx\)をテイラー展開すると
$$sinx=\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+・・・$$
両辺を\(x\)で割ると
$$\frac{sinx}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+・・・$$
これを頭の隅に置いておいて
$$sinx=0$$
としたとき、右辺が\(0\)になるような\(x\)は
$$x=0, +\pi, -\pi, +2\pi, -2\pi, +3\pi, -3\pi, ・・・$$
とたくさんある。これらが\(x\)に代入されたとき、いつでも右辺が\(0\)となるようにするためには
$$sinx=x(x+\pi)(x-\pi)(x+2\pi)(x-2\pi)(x+3\pi)(x-3\pi)・・・$$
となってあるべきだ。試しにどれか代入してみたらいいと思う。どこかのカッコが\(0\)になるので、方程式を満たしていることがわかるはずだ。
他にこんなのはどうだろうか
$$sinx=x\bigg(1+\frac{x}{\pi}\bigg)
\bigg(1-\frac{x}{\pi}\bigg)
\bigg(1+\frac{x}{2\pi}\bigg)
\bigg(1-\frac{x}{2\pi}\bigg)
\bigg(1+\frac{x}{3\pi}\bigg)
\bigg(1-\frac{x}{3\pi}\bigg)
・・・ $$
結局、\(x=n\pi\)という数値が代入されたとき、カッコのどれかが\(0\)になればいいわけで、この形でも問題ないはずなのだ。
さらに\(x\)で割ってやると
$$\frac{sinx}{x}=\bigg(1+\frac{x}{\pi}\bigg)
\bigg(1-\frac{x}{\pi}\bigg)
\bigg(1+\frac{x}{2\pi}\bigg)
\bigg(1-\frac{x}{2\pi}\bigg)
\bigg(1+\frac{x}{3\pi}\bigg)
\bigg(1-\frac{x}{3\pi}\bigg)
・・・ $$
ここから右辺の1つ目のカッコと2つ目のカッコ、3つ目のカッコと4つ目のカッコ、5つ目のカッコと6つ目のカッコ・・・とそれぞれかけてあげると
$$\frac{sinx}{x}=
\bigg(1-\frac{x^2}{\pi^2}\bigg)
\bigg(1-\frac{x^2}{2^2\pi^2}\bigg)
\bigg(1-\frac{x^2}{3^2\pi^2}\bigg)
・・・ $$
これで2種類の\(\frac{sinx}{x}\)の式が出来た。これをイコールでつなげると
$$ \bigg(1-\frac{x^2}{\pi^2}\bigg)
\bigg(1-\frac{x^2}{2^2\pi^2}\bigg)
\bigg(1-\frac{x^2}{3^2\pi^2}\bigg)
・・・ =
1\color{blue}{-\frac{x^2}{3!}}+\frac{x^4}{5!}-\frac{x^6}{7!}+・・・ $$
右辺でひとつの項だけ目立たせたのは、後で係数の比較をするためだ。
これから左辺をアレンジしていくのだけど、それぞれのカッコの右側の分数がごちゃごちゃしてるので左から\(x^2\)以外の部分を簡単な文字に置き換える。
$$a=-\frac{1}{\pi^2}, \
b=-\frac{1}{2^2\pi^2} ,\
c=-\frac{1}{3^2\pi^2} , \
d=-\frac{1}{4^2\pi^2} $$
というふうに置き換えて左辺を展開すると
$$(1+ax^2)
(1+bx^2)
(1+cx^2)
(1+dx^2)・・・ $$
$$=(1+(a+b)x^2+abx^4)(1+cx^2)(1+dx^2)・・・$$
$$(1+\color{pink}{(a+b+c)x^2}+(ab+ac+bc)x^4+abcx^6)(1+dx^2)・・・$$
ひとつずつ展開していって、ピンク色の\(x^2\)の前の係数に注目すると、展開するごとに文字が\(a+b+c+・・・\)と増えていくのがわかる。これらの文字を元の分数に直して、ピンク色の部分だけ抜き出せば
$$\bigg(-\frac{1}{1^2\pi^2}
-\frac{1}{2^2\pi^2}
-\frac{1}{3^2\pi^2}
-\frac{1}{4^2\pi^2} ・・・\bigg)x^2$$
となる。ここで、さっき係数を比較するために青色に目立たせていたところを注目しよう。この青い部分も\(x\)の方に乗っている指数が\(2\)なので、ピンク色の\(x^2\)の係数と青色の係数が同じでなくてはならないので
$$\bigg(-\frac{1}{1^2\pi^2}
-\frac{1}{2^2\pi^2}
-\frac{1}{3^2\pi^2}
-\frac{1}{4^2\pi^2} ・・・\bigg)x^2=-\frac{1}{3!}x^2$$
から\(x^2\)を除いて、符号を整えると
$$\frac{1}{1^2\pi^2}
+\frac{1}{2^2\pi^2}
+\frac{1}{3^2\pi^2}
+\frac{1}{4^2\pi^2} ・・・=\frac{1}{6}$$
さらに両辺に\(\pi^2\)をかけると
$$\frac{1}{1^2}
+\frac{1}{2^2}
+\frac{1}{3^2}
+\frac{1}{4^2} ・・・=\frac{\pi^2}{6}$$
これが導出だ。やはりこの数列から\(\pi\)が出てくるのが不思議でたまらない。




コメント