状態量と完全微分

熱力学を勉強していると状態量（State Quantity）という言葉によく出会う。

状態量と呼ばれているものには、こういったものがある。

温度($T$)、体積($V$)、圧力($P)$といった基本的なものの他に、内部エネルギー($U)$、エントロピー($S)$、エンタルピー($H)$やヘルムホルツの自由エネルギー($F)$とギブスの自由エネルギー($G)$も状態量である。特に後ろの２つは状態量だから重要というよりか、状態量になるようにして作られた指標というイメージが強い。

状態量というのは変化のさせ方によらず、ある状態ならいつも同じ値を取るものである。

わかりにくいと思うので、状態量でないものの代表、仕事($W)$を使って確認してみよう。ちなみに熱($Q)$なんかも状態量でないものだ。

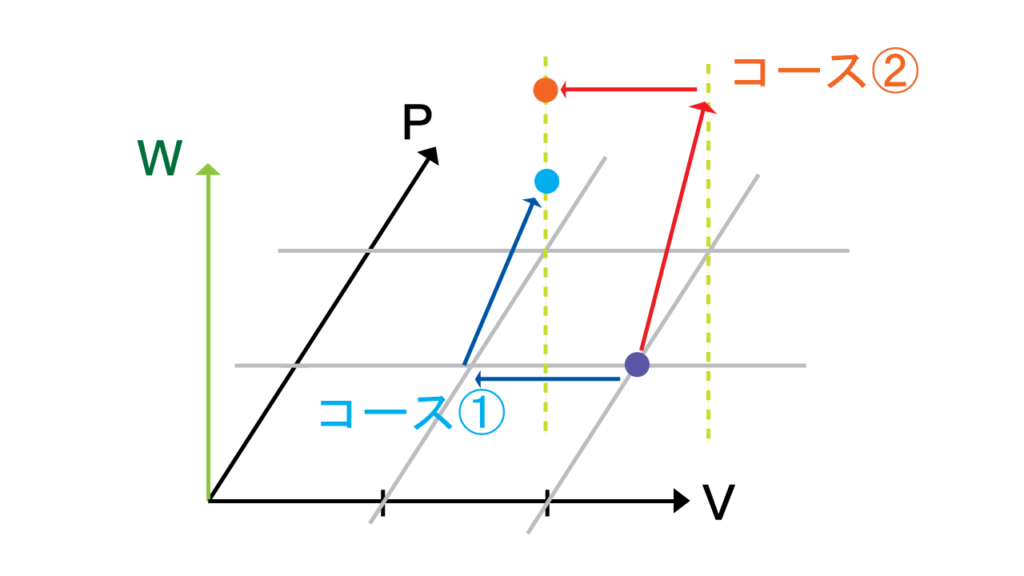
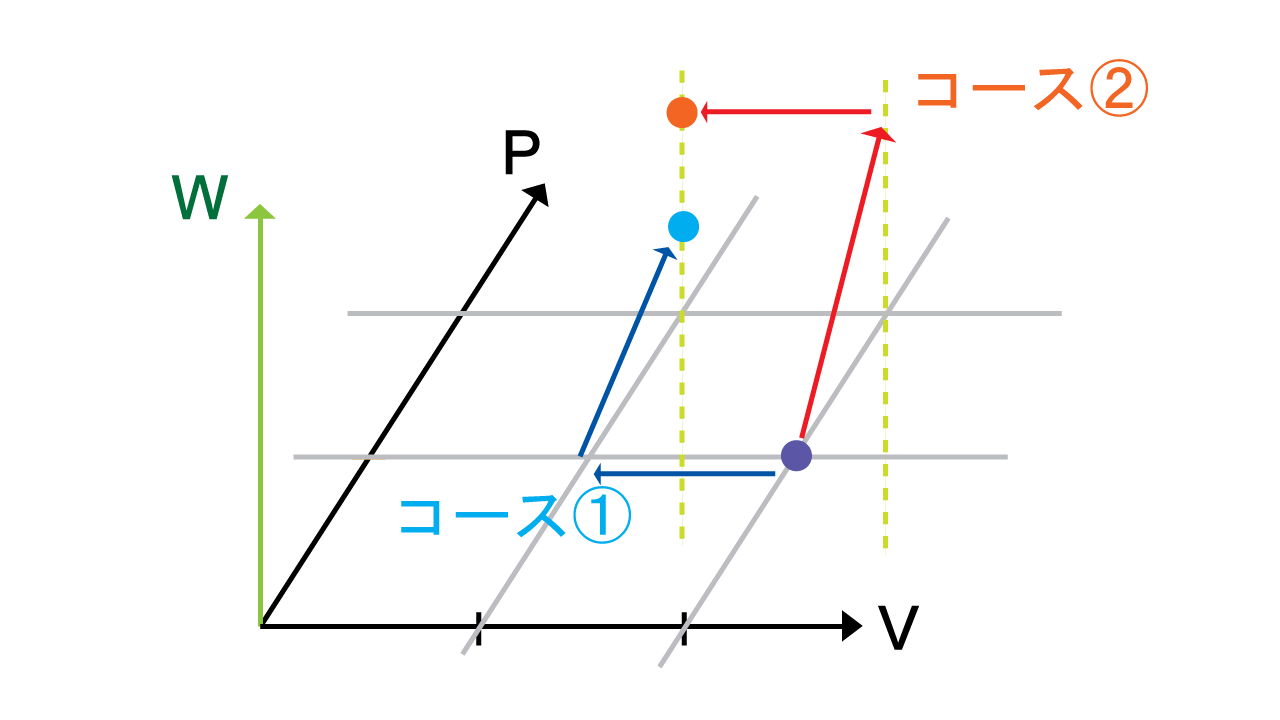
例　初めの状態（$P_i=1[Pa]$と$V_i=2[V]$）を次の状態（$P_f=2[Pa]$と$V_f=[1V]$）に持っていくときの道のりを考える。経路はいろいろあるけども、ここでは①$P=1[Pa]$で保ったまま$２[V]$を$１[V]$まで圧縮するしてから、$V=1[V]$で固定して$１[Pa]$を$２[Pa]$にもってくるコースと②今度は$V=2[V]$で固定して$1[Pa]$を$2[Pa]$まで上げてから、そのあと圧力を$2[Pa]$で保ちながら$2[V]$から$1[V]$に圧縮するコース、という2つの経路について考えてみたい。

コース①仕事の計算は$W=-P\Delta V$を使う。まず「$P=1[Pa]$で保ったまま$２[V]$を$１[V]$まで圧縮する」というのは

$$W_i=-(1[Pa])(1[V]-2[V])=1[J]$$

「$V=1[V]$で固定して$１[Pa]$を$２[Pa]$にもってくる」という次の工程は

$$W_f=-(2[Pa]-1[Pa])(1[V]-1[V])=0[J]$$

仕事はその体積が変わらなければ０である。よってコース①のトータルの仕事量は

$$W_{total}=W_i+W_f=(1)+0=1[J]$$

である。

次はコース②を計算してみよう。

「$V=2[V]$で固定して$1[Pa]$を$2[Pa]$まで上げる」というのは、その過程で体積が変化していないので仕事は０である。

$$W_i=0$$

「圧力を$2[Pa]$で保ちながら$2[V]$から$1[V]$に圧縮する」というのは

$$W_f=-(2[Pa])(1[V]-2[V])=2[J]$$

よってコース②のトータルの仕事量は

$$W_{total}=W_i+W_f=(0)+(2)=2[J]$$

他にもコースのたどり方はいくつもあるが、この単純な２つのコースでも結果が違うのがよくわかると思う。

なぜこうなるのか数学的にいうと、仕事は不完全微分だからである。

不完全微分？また変な名前が出てきた。

（不完全）微分という言葉が出てきたが、これは熱力学にとってとっても重要なコンセプトで、２つ以上の変数を微分形式で扱うときに完全微分か不完全微分になるかで話が大きく変わってくる。ちなみに状態量というものは全て完全微分で表される。

まず初めに変数が２つ以上の時の微分はどうするかについて考えなければならない。

２つ以上の変数がある場合、微分をするときに全微分という形式で微分されなければならない。さらにその全微分の形式の中である性質を満たしているものが完全微分と言われる。

ここでは全微分の導出についてはしないことにする。Google検索で「全微分とは」と調べればよい記事がたくさん出てくるはずだ。そんなことよりも物事と物事のつながりを大切にしたい。いづれ余力があれば書くかもしれないけども。

ともかく全微分というのは、もし$x$と$y$という２つの変数を持つ$z(x,y)$を微分するとき、次のように表される。

$$dz=\bigg(\frac{\partial z}{\partial x}\bigg) dx + \bigg(\frac{\partial z}{\partial y}\bigg) dy$$

さらに

$$\bigg(\frac{\partial z}{\partial x}\bigg)=\bigg(\frac{\partial z}{\partial y}\bigg) $$

を満たすとき、完全微分と呼ばれる。これが状態量が状態量であるための満たされるべき数学的要請だ。

仕事（$W$\）で試してみよう。

仕事（$W$）は圧力（$P$）と体積（$V$)の関数であるといえるので、$z(x, y)$の代わりに$W(P, V)$として全微分形式で書いてやると

$$dW=\bigg(\frac{\partial W}{\partial P}\bigg) dP + \bigg(\frac{\partial W}{\partial V}\bigg) dV$$

となる。文字を入れ替えただけだ。全微分の形は覚えてしまったほうが良さそうだ。そうすれば、変数が２つ以上の時それらをxとyをその２つの変数に変えればいいだけになる。

上のように全微分形式で書いたわけだけど、ちょっと注意しなければならないことがある。それは右辺１項目の$\partial W/\partial P$が０になるということだ。なぜならそれは偏微分なのでもうひとつの変数Vは定数として扱うので、$\Delta V=0$となり仕事量WはPがどれだけ変化しようと０となる。結局さっきの全微分は

$$dW=(0)dP+\bigg(\frac{\partial W}{\partial V}\bigg)dV=\bigg(\frac{\partial W}{\partial V}\bigg) dV $$

となる。これを積分すると仕事$W$を計算できるのだ。ちなみにちゃんと書くと

$$W=\int dW=P \int_{V_i}^{V_f}dV$$

である。ときどきこうやって基本的なことを確認することはいいことだ。

この仕事の全微分形式は

$$\bigg(\frac{\partial W}{\partial P}\bigg)\neq \bigg(\frac{\partial W}{\partial V}\bigg)$$

なので、これは状態量と呼ばれるべきではないのだが、なぜ直前の式が$＝$で結ばれるときコースに限らず結果が決まるのかという数学的な理解をまだできていないので、それはまた別の機会に行いたいと思う。