
Definition of dot product
$$\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos{\theta}$$
We should not think dot product is nature thing in the world.
It could be the one that we created for use.
So understanding of the meaning of dot product is not easy.
If I have to choose one for it, I would choose “Similarity of the 2 vectors”.
You might not get it at all. Let’s talk about the deviation of it first and think of the meaning.
Cosine Rule
Dot product comes from Cosine Rule.
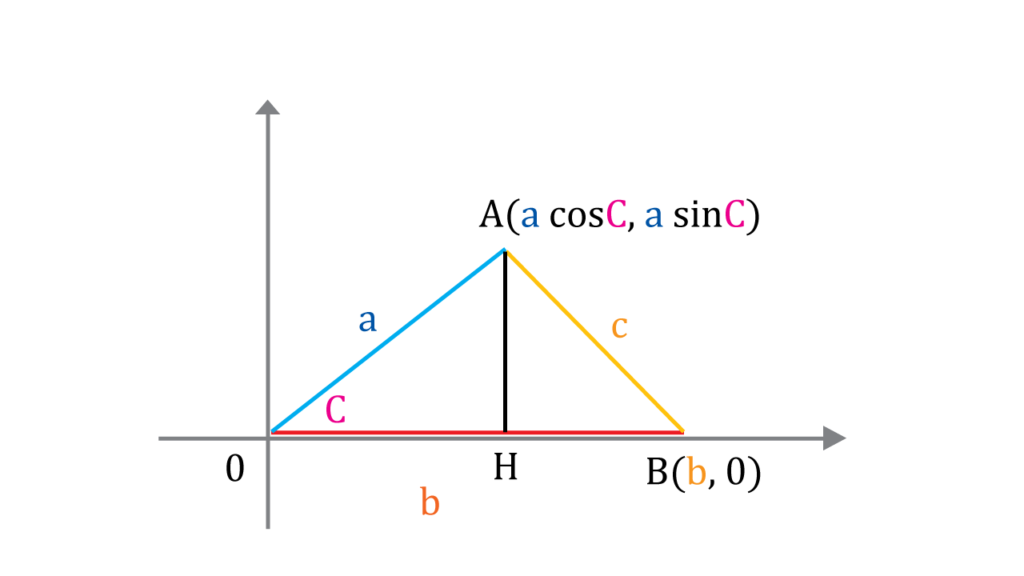
If you focus on the right side of the right triangle and use Pythagorean Theorem.
$$c^2=(b-a\cos{C})^2+(a\sin{C})^2$$
$$=b^2-2ab\cos{C}+a^2\cos^2{C}+a^2\sin^2{C}$$
$$=b^2-2ab\cos{C}+a^2(\sin^2{C}+\cos^2{C})$$
Therefore
$$c^2=a^2+b^2-2ab\cos{C}$$
We decided to express \(ab\cos{C}\) by another way which is called dot product. From this equation if you have a big angle of \(C\), you would have large value of \(c\).
In another way, the directions of the 2 vectors making the angle C are pointing toward different ways. The similarity of the 2 vectors is small.
If you have a small angle \(C\), then you would have small value of \(c\). So the vectors are pointing to same direction. The similarity of the 2 vectors is large.
In order to make the new value “Similarity of 2 Vectors”, we defined \(\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos{\theta} \). It would be hard for beginners to understand how important it is now. However, we will know how useful it is as we learn physics further.
Anyway we now know
$$\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos{\theta} $$
There is another form of equations for dot product.
If \(\vec{a}=(x_1, y_1)\ and\ \vec{b}=(x_2, y_2)\), then
$$\vec{a}・\vec{b}= x_1 x_2 + y_1 y_2 $$
This time we are not using any angle to calculate dot product.
Deviation
It also comes from Cosine Rule
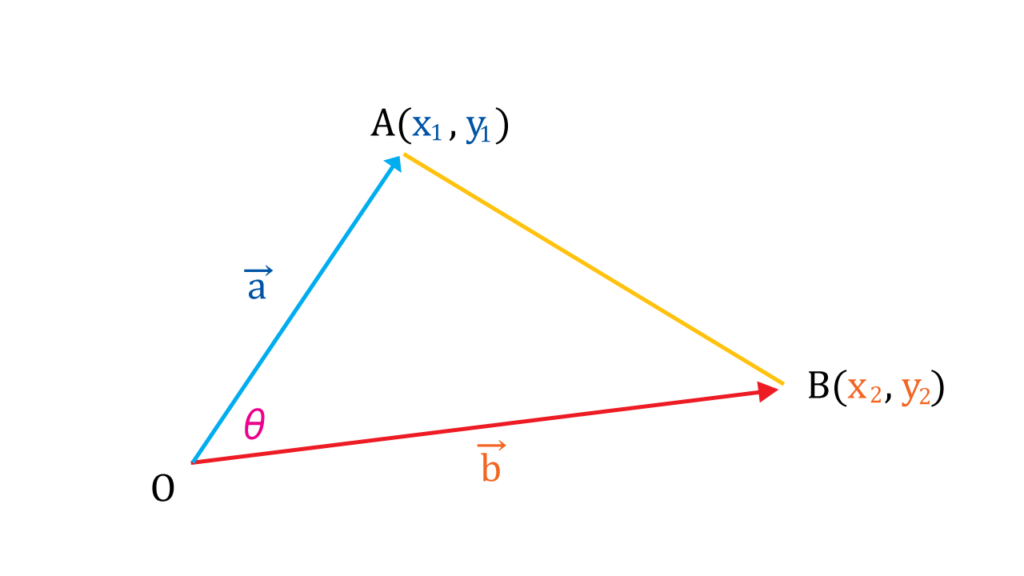
$$AB^2 = OA^2 + OB^2 -2(OA)(OB)\cos{\theta}$$
since coordinates of point A and B are
$$A=(x_1,\ y_2)\ and\ B=(x_2,\ y_2)$$
Also using the first equation for dot product for the third term on the right hand side \(
-2(OA)(OB)\cos{\theta} \)
Then
$$(x_2-x_1)^2 + (y_1-y_2)^2 = (x_1^2+y_1^2)+(x_2^2+y_2^2)-2\vec{a}・\vec{b}$$
If we arrange this, it is going to be
$$\vec{a}・\vec{b}= x_1 x_2 + y_1 y_2 $$
Let’s check if both of formulas could get same result.
Example



コメント