Purpose: Calculate The Age of The Universe with Hubble’s Law
Hubble is the name of a science. He is the one who found out the size of the universe is expanding. Einstein who believed that the universe was static introduced Cosmological Constant in order to make his equation of the universe static. However, he thought introducing Cosmological Constant was his biggest blunder in his life because of Hubble’s discovery.
Hubble who observed the universe with a telescope discovered that the more distant a celestial body, the faster it was receding. The following graph is about it.
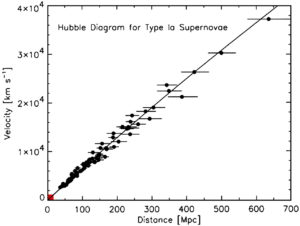
Each black dot indicates each celestial body.
The horizontal axis is “The Distance between The Earth and Each Celestial Body”, the vertical axis is “The Receding Velocity of Each Celestial Body”.
If you see more distance celestial body, it has larger receding speed.
This simple graph can be written in a basic equation.
$$v=H×r$$
If we use English for it
$$”The\ Receding\ Speed\ of\ The\ Celestial\ Body”$$ $$=H(Hubble\ Constant)$$ $$×$$ $$”The\ Distance\ between\ The\ Celestial\ Body\ and\ The\ Earth”$$
The slope of the lie on the graph is the H (Hubble Constant).
Currently, the value of the Hubble Constant is supposed to be about \(70.5km/(s・Mpc)\). You might wonder of \(「Mpc」\). But things are not such difficult. It is a different unit of distance, which is called “Mega Parsec”. If we convert it to meter, it is \(3.09×10^{22} m\). Cosmologists use another unit due to the much larger size of the universe than the earth.
Since both \(m\) and \(Mpc\) are unit for distance, we can make them be cancelled out. The remaining unit is \(1/s\). So, Hubble Constant’s unit is the reciprocal of time.
$$H=70.5\frac{km}{s・Mpc}\times \frac{1000m}{km}\times \frac{Mpc}{3.09 \times 10^{22}m}=2.28 \times 10^{-18} (\frac{1}{s})$$
We might be surprised with this fact, but it is an obvious thing if considering carefully.
For example, let’s express the equation for the speed of a car. Then,
$$The\ Speed\ of\ the\ car=\frac{Distance\ The\ Car\ Has\ Driven}{Time\ The\ Car\ Has\ Spent}$$
It is shown with the fraction, so it might look a little bit confusing. However, if using multiplication for it, it could be more clear than this.
$$The\ Speed\ of\ the\ car=\frac{1}{Time\ The\ Car\ Has\ Spent}\times Distance\ The\ Car\ Has\ Driven$$
How about this expression. the unit of the fraction of the right side of this equation becomes \(1/s\). This equation looks alike with Hubble’s Law \(v=H×r\). The Hubble’s Law contains the fancy, Hubble Constant, but what it does is similar to the equation for the speed of the car.
Actually, strictly speaking, those are not same things because the reasons of those celestial bodies receding are the expanding of the space of the universe. A rising loaf of raisin bread is a good visual model. Each raisin will see all other raisins moving away from it as the loaf expands.
Even though those reasons are different, if we take the reciprocal of Hubble Constant, we could get about time how much the universe has spent from the beginning. It seems to go well. Let’s take the reciprocal of Hubble Constant and convert the unit to \(Year\).
$$\frac{1}{H} \frac{s}{1}×\frac{min}{60s}×\frac{hour}{60mins}×\frac{day}{24hours}×\frac{Year}{365days}$$
$$=1.39×10^{10}Years$$
As a matter of fact, the expansion of the universe seems to be accelerating, so the value of the result would be different. However, more important thing is that the way to think of calculating the age of the universe is not that complicated, and we could get the appropriate value for the age with assuming the expanding speed is constant.



コメント