宇宙の年齢を計算してみようという記事の中で、ハッブルがたくさんの天体の距離を測った訳だけど、実際どうやって遠くにある星までの距離を測ったのだろうか。
記事の中で紹介した図には「Hubble Diagram for Type 1a Supernovae」と記載されてあるので、Ⅰa型超新を使って距離を調べたと思われる。これは後で紹介するけども、天体の中でもより遠くにあるものの距離を測定するのに使われる手法である。
実は地球から天体までの距離を求める方法は距離によって様々ある。
まず人類が一番初めに測った距離の天体は月だろう。
幾何学を用いて距離を測る
月までの距離
紀元前\(3\)世紀、当時は月の大きさ(約\(3200km\))をすでに把握していたので、それを使って月までの距離を測定した。月を片目だけで見上げて、腕を伸ばし、指の先で月を覆うようにして、爪の上下と目を結んでできる三角形を作る。その三角形は、月の直径の両端と目を結ぶ三角形が相似であり、腕の長さと爪の長さの比が月までの距離と月の直径との比と等しいことを利用して、月までの距離を求めた。
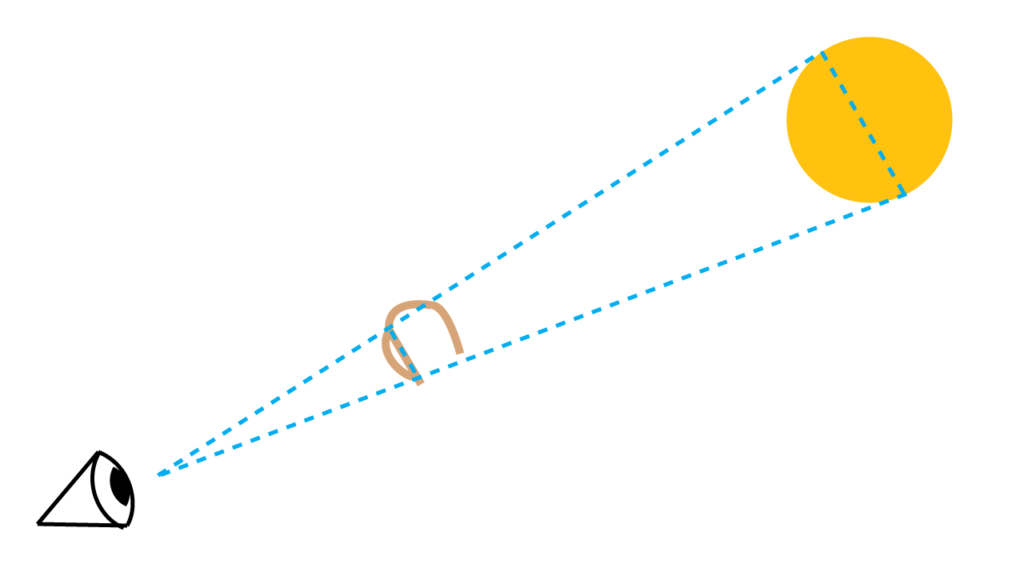
腕の長さと爪の長さの比は大体\(100\)対\(1\)なので、月までの距離と月の直径の比も\(100\)対\(1\)だとすると、\(3,200km×100=320,000km\)となる。
太陽までの距離
月は太陽の光を反射して光っているということは当時すでに知られていて、それが正しいとすると、半月になるのは太陽と月と地球が直角三角形の配置になったときだと考えて、計算された。
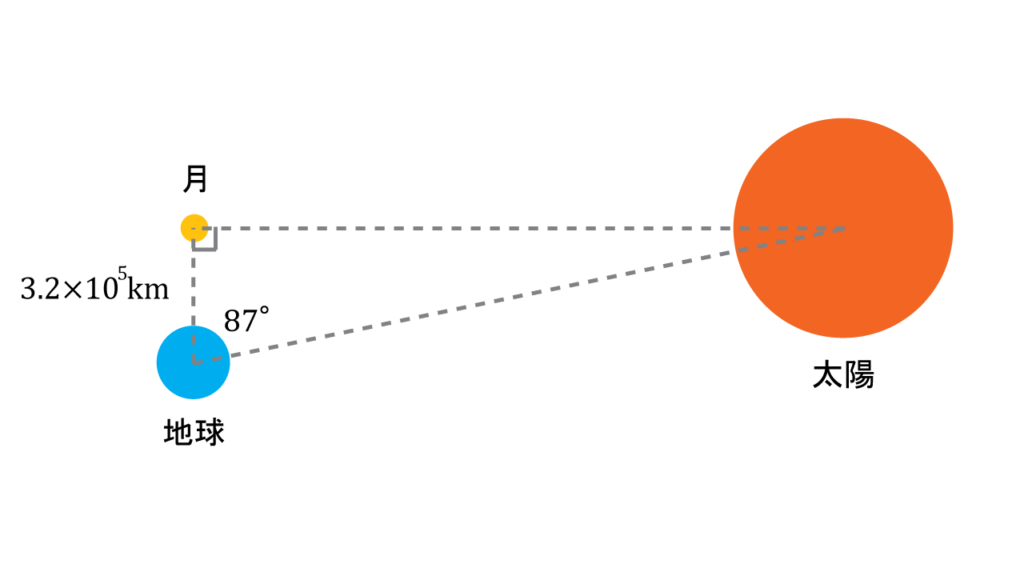
この時の、地球と月を結ぶ線と地球と太陽を結ぶ線の成す角度が\(87\)度(実際は\(89.85\)度)として計算されていた。この角度を測るのが一番苦労したかもしれない。だってこの瞬間に影のできない建物や地面に突き立てた棒の場所を発見しなければならないから。
銀河系内の比較的近い天体までの距離(100光年先ぐらいまで)
三角形を作って距離を測るというのはいろいろなところで使われていて、さっきの月や太陽までの距離を測るときも、その地点まで行かなくても\(2\)辺の距離や\(1\)辺の距離と角度という他の情報から一番欲しい距離を計算することができた。
年周視差
これと似たような方法で銀河系の中の比較的近い天体の距離(\(100\)光年以内まで)を調べることができる。それが年周視差(\(Stellar\ Parallax\))という方法だ。
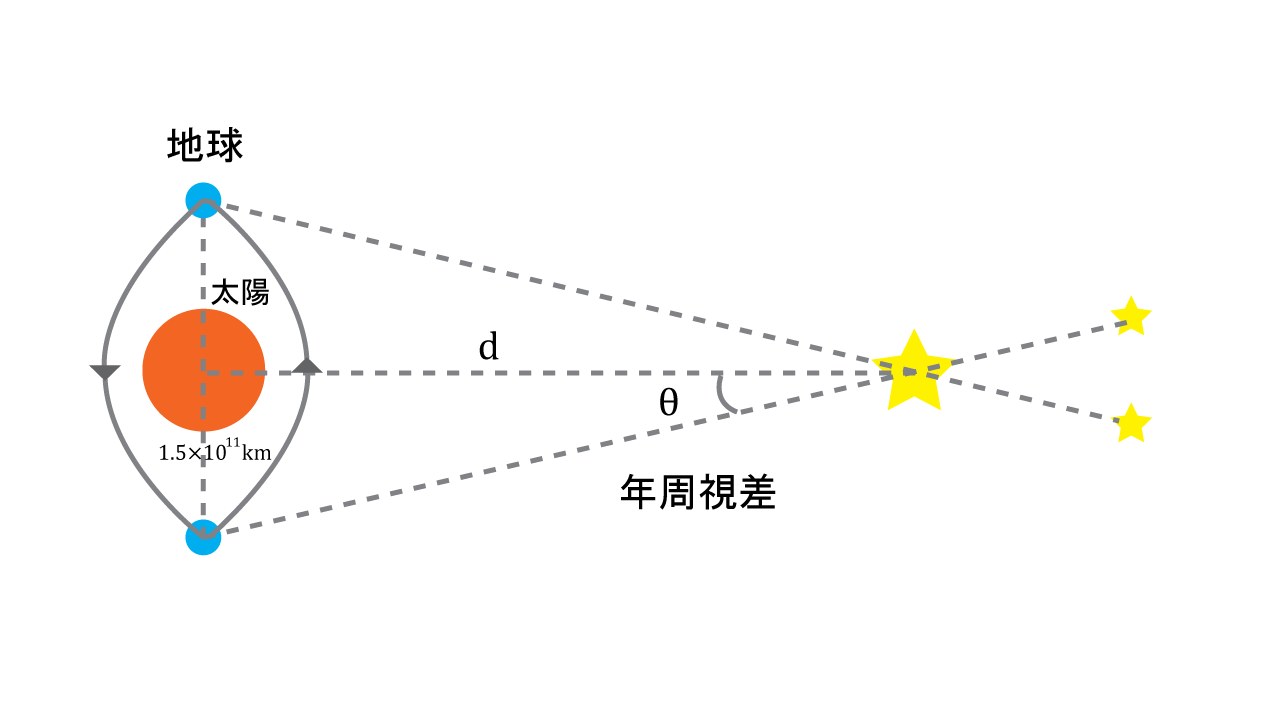
人間も左目と右目が離れている分、物の位置つまり視線の方向が異なる。この「視差」という現象を使って僕たちは物の距離を測っているように、ある時点からの視点と、そこからちょうど半年後、つまり太陽の周りを半周した地点からの視点の視差を用いて距離を測るのだ。
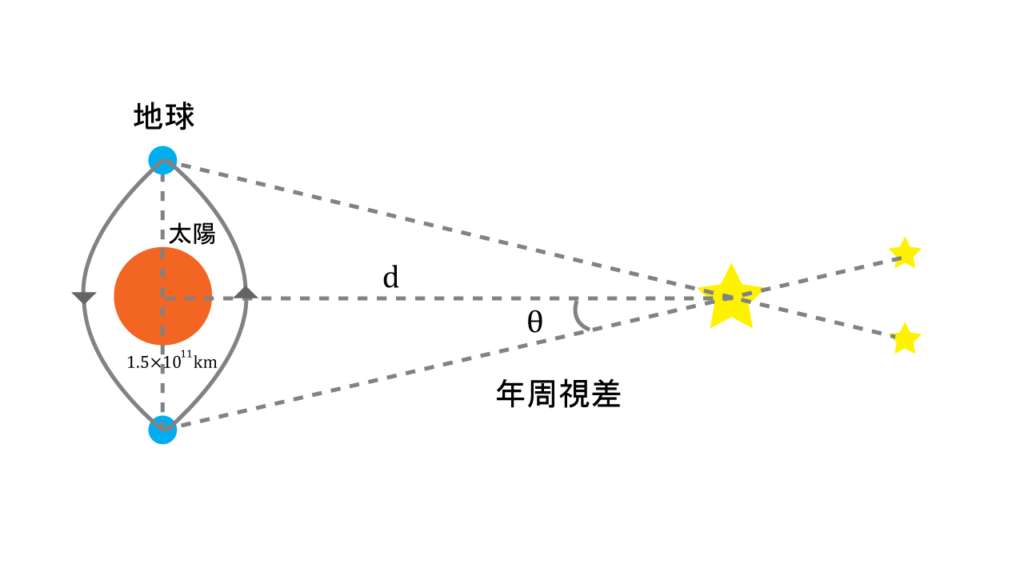
この太陽と地球までの距離は\(1AU\)という天文単位で約\(1.5×10^{11}m\)だ。あと年周視差の角度さえわかれば、天体までの距離を\(d\)と置いて
$$tan\theta=\frac{1AU}{d}$$
から、\(d\)について解いて
$$d=\frac{1AU}{tan\theta}$$
の式から、距離を計算することができる。
ちなみに天文学でよく使われるパーセクという距離の単位は\(parallax\ second\)から来ていて、\(1\ parsec\)は年周視差が\(1\)秒角(1/3600 degree)になる距離と定義されている。メートルで表すと\(3.086×10^{17}m\)である。
人間の場合、\(20km\)先のものを両目で見ると視差が約\(1\)秒角と言われている。
天体の色から距離を測る
銀河系の中の遠い天体(10万光年以内)
\(100\)光年以上の距離になってくると、地球と太陽が作る年周視差は小さすぎて距離が正確に測れなくなってくるようだ。そこで使われるのが、星の色から距離を測るという方法だ。
明るさというのは距離の\(2\)乗に反比例して小さくなっていくのだが、色自体は距離があっても変わらない。例えば、とても暗い天体があって、それが太陽と同じ色をしていたとしたら、その天体の実際の明るさは太陽と同じであるといえる。
全然関係ない話になってしまうが、明るさだけでなく万有引力やクーロン力といったものも距離の\(2\)乗に反比例して力が小さくなっていく。これらを逆\(2\)乗型の法則というらしいのだが、個人的に非常に興味がある。これに関わるいくつか計算があって、時間があるときにじっくりやってみたい。
明るさ
意識しないといけないことは、明るさには\(2\)種類あるということだ。見かけの明るさと絶対等級だ。見かけの明るさというのは、夜に空を見上げた時に私たちが感じる明るさのことで、上で言ったように地球から遠い星ほど見かけの明るさは小さくなっていく。絶対等級というのは、その天体が実際に輝いている光の強さのことである。絶対等級の方が大切やん、と思うかもしれないけど、明るさは距離の\(2\)乗に反比例して小さくなるという性質を利用して、その天体までの距離を測ることができているので、どっちがどっちという話ではない。
絶対等級
絶対等級は本当の天体の明るさということだったけど、どこから測った明るさなのだろうか。実は定義があって
天体を10pcの距離から見たときの等級
ということのようだ。これは後程使う。
具体的にはHR図と呼ばれる縦軸を絶対等級(明るさ)横軸を表面温度(色)に取ったグラフを用いてその絶対等級を推定し、そこからポグソンの式を用いて距離を計算する。
ポグソンの式
星\(1\)の等級を\(m_1\)、明るさをフラックス\(F_1\)、もうひとつの星\(2\)の等級を\(m_2\)、明るさを\(F_2\)とすると
$$m_1-m_2=-\frac{5}{2}\log_{10}{\frac{F_1}{F_2}}$$
のように表すことができる。これがポグソンの式である。
距離を測定する場合はこれを少し変形させて使うのだけど、その前にこれがどのように導出されたのか見てみよう。
ポグソンの式の導出
実際の光度を\(L\)とし、見かけの明るさ(フラックス)\(F\)は距離\(r\)の\(2\)乗に反比例するというのを式で表すと、
$$F=\frac{L}{4\pi r^2}$$
となる。天体の光は\(1\)点から全方向に満遍なく放射されるので、\(4\pi r^2\)という球体の表面積の式が表れる。
また同じ天体(光度L)を距離(r)の違う場所から観測すれば、見かけの明るさ\(F\)も違ってくる。ひとつを\(F_1\)、もうひとつを\(F_2\)と置くと
$$F_1=\frac{L}{4\pi r_1^2}$$
$$F_2=\frac{L}{4\pi r_2^2}$$
とそれぞれ表される。
この\(F_1\)と\(F_2\)の比をとると
$$\frac{F_1}{F_2}=\frac{L}{4\pi r_1^2 }\frac{4\pi r_1^2 }{L}=\bigg(\frac{r_2}{r_1}\bigg)^2$$
もし星\(1\)の明るさを絶対等級とするなら、絶対等級の定義「天体を\(10pc\)の距離から見たときの等級」から星\(1\)までの距離\(r_1=10pc\)と設定しなければならない。すると
$$\frac{F_1}{F_2}=\bigg(\frac{d\ pc}{10\ pc}\bigg)^2$$
\(m_1\)は今は絶対等級であることを意識するために\(M\)に置き換えて、\(m_2\)は地球からの見かけの明るさということで\(m\)にし、ポグソンの式にこれらを代入すると
$$M-m=-\frac{5}{2}\log_{10}{\bigg(\frac{d}{10}\bigg)^2}$$
対数の計算の法則を使って
$$=(2)\bigg(-\frac{5}{2}\bigg)(\log_{10}{d}-\log_{10}{10})$$
となる。\(log_{10}{10}\)というのは\(0\)なので
$$M-m=-5\log_{10}{d}$$
$$M=m-5\log_{10}{d}$$
$$\log_{10}{d}=-\frac{M-m}{5}$$
$$d=10^{-\frac{M-m}{5}}$$
見かけの明るさ\(m\)からHR図を使って天体の絶対等級\(M\)がわかれば、この式を使ってその天体までの距離を計算できるのである。
銀河系外の天体
私たちがいる銀河の外にあるような天体の距離を測るのも基本的には上で説明したように、見かけの明るさと絶対等級の関係から距離を測る。
セファイド
セファイドとは膨張と縮小を規則正しく繰り返している天体で、それに伴って明るさも規則正しく変化している。この変更周期から絶対等級を算出できるらしい。
Ⅰa型超新星
さらに遠くの天体の距離を測るときはⅠa型超新星という特別な超新星を扱う。こちらもセファイドと同じように明るさが規則的に変化するのだが、このⅠa型超新星は最も明るくなった時の絶対等級が同じであるという性質がある。



コメント