Quadrature by Parts

Quadrature by Parts (区分求積法)

This is very similar way to calculate the area by Integration

Let’s take a look the formula first

$$\int^1_0 f_{(x)}dx = \lim_{x \to \infty} \frac{1}{n} \bigg\{ f_{(\frac{1}{n})}+
f_{(\frac{2}{n})} + … +
f_{(\frac{n}{n})} \bigg\}$$

$$= \lim_{x \to \infty} \frac{1}{n} \sum^{n}_{k=1} f_{(\frac{k}{n})}$$

If you have a graph of $y=x^2$ and calculate the area enclosed by the graph and x axis, you usually use integration to calculate it.

Let’s calculate it with the range ($0≦x≦1$)

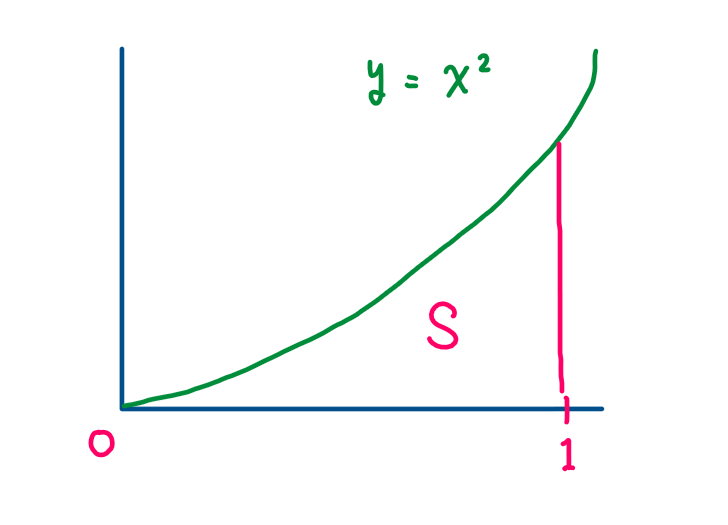
$$S=\int_0^1 x^2 dx
= \bigg[\frac{1}{3} x^3 \bigg]^1_0
= \frac{1}{3}$$

It is time to learn another way to calculate the area with Quadrature (Mensuration) by Parts.

The idea is following.

We put some bars along the graph (10 bars this time) like the picture below.

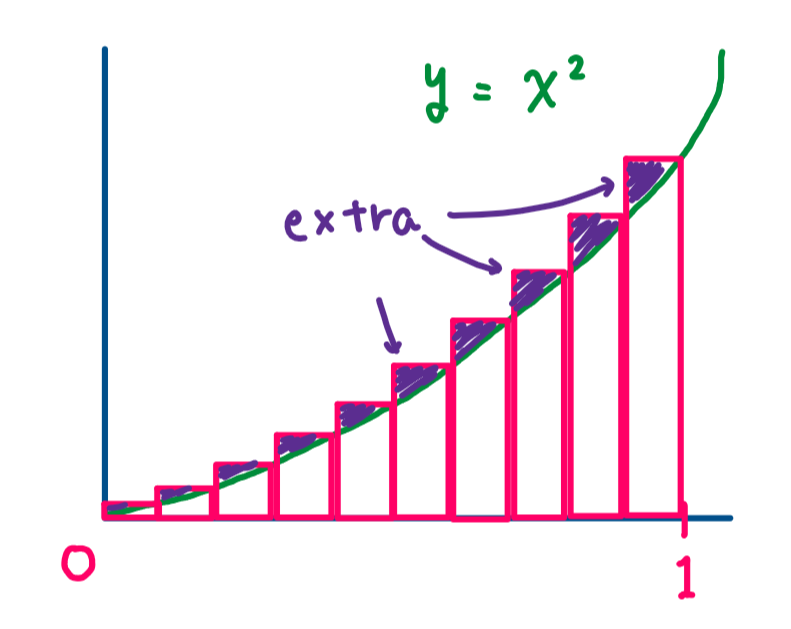
Since the equation of the graph is $y=x^2$, each vertical lengths of bars are

$$\bigg(\frac{1}{10} \bigg)^2,\
\bigg(\frac{2}{10} \bigg)^2,\
\bigg(\frac{3}{10} \bigg)^2,\ …
\bigg(\frac{10}{10} \bigg)^2\ $$

Therefore, total area of the bars is

$$S=\bigg(\frac{1}{10}\bigg)^2 × \frac{1}{10}
+\bigg(\frac{2}{10}\bigg)^2 × \frac{1}{10}
+\bigg(\frac{3}{10}\bigg)^2 × \frac{1}{10}
+ … +
\bigg(\frac{10}{10}\bigg)^2 × \frac{1}{10} $$

$$=\frac{385}{1000}=\frac{77}{200}≈\frac{1}{3}$$

The reason why we could not get the exact same value with $\frac{1}{3}$ from Integration is that there are some extra areas above the graph.

Now Let’s consider of more general equation of it.

We make $n$ bars instead of 10 bars. Then the equation for the area would be

$$S=\bigg(\frac{1}{n}\bigg)^2 × \frac{1}{n}
+\bigg(\frac{2}{n}\bigg)^2 × \frac{1}{n}
+\bigg(\frac{3}{n}\bigg)^2 × \frac{1}{n}
+ … +
\bigg(\frac{n}{n}\bigg)^2 × \frac{1}{n} $$

Using $\sum$

$$=\frac{1}{n^3} \sum^n_{k=1}k^2$$