
エントロピー
エントロピーは熱力学において重要な示量のひとつである。
時として「乱雑さ」や「情報量」といったものに言い換えられて扱われているかもしれない。
しかしこれを聞くといつも疑問が頭によぎる。
熱力学という熱や温度といったものに関するものなのに、なぜエントロピーは「乱雑さ」や「情報」という熱力学に関係なさそうな名前がついているのだろうか。
どうやらそれらは長い年月をかけて解釈された結果であって、もともとは熱や温度にかかわる示量であるようだ。
実際、エントロピーは\(S\)という文字を使って
$$dS = \frac{dQ}{T}$$
という風に熱\(Q\)と温度\(T\)が式の中に組み込まれている。
この式からエントロピーとは何ぞやということを考えるのは難しいから、まずはエントロピーという概念が誕生した背景を辿るとわかりやすいかもしれない。
クラウジウスの原理
エントロピーはクラウジウスの原理を発端にしている。
クラウジウスは
低温の熱源から高温の熱源に正の熱を移す以外に、他に何の痕跡も残さないようにすることは出来ない。
と言ったらしい。訳のわからない文章を分析するのは置いていて、要は
熱は高温部分から低温部分に向かって自然に移動する
ぐらいの理解でいいと思う。
ちょっとエントロピーの話から逸れるけども、いろいろな本を読んでいると、「熱」というのはエネルギーの移動の手段であるから、熱が移動するという表現は正しくないとかなんちゃら…ということが書いてあったりする。これまで深く考えたことなかったけど、何となくイメージの中で空間の中に熱という温度を保有する塊のようなものを考えてしまうけど、実際はそうではないようだ。
しかし僕は学者でも何でもないので、そのような細かい部分は省略する。ここでは難しい概念や数式を何となくイメージできるぐらいになるのが目的だ。(ちゃんと理解してないだけなんだけども(笑))そんな細かいところまでやってたら、物理学を勉強するのに僕のような凡人では命がいくつあっても足りないでしょ。
ともあれ、温かいお茶を机の上にしばらく置いていたら、だんだん冷えて部屋の温度と同じくらいになるのは日常的に経験する。物理学的には熱が逃げるという表現は正確じゃないかもしれないけども、今はそれでも問題はないように思える。あと「自然に」という言葉を付けたのは、その逆の移動は起こらない。つまり、冷めたお茶がひとりでに温まったりしないということだ。
違った表現をすれば、このクラウジウスの原理は火を使って加熱したりという外部からの働きがなければ、熱(エネルギー)は暖かいところから冷たいところに流れるというのが自然の原理だということだ。
これがどうエントロピーという概念になっていくのか。まずはさっきの式がどのようにして導かれたかを知らなければならない。
カルノーサイクル
カルノーサイクルは等温変化と断熱過程で組み合わされた理想的な熱サイクル(熱機関)と言われている。
熱サイクルでは石炭などを燃やして熱を発生させて、ピストンを動かして動力を得る。
その昔、当時の技術者たちはどうすれば効率よく熱から動力を得るか必死になって考えていた。
はじめの熱を\(Q_1\)、得られる動力を\(W\)、動力に成り得ず放出される熱を\(Q_2\)とすれば、カルノーサイクルの熱効率\(\eta(エータ)\)は
$$\eta=1-\frac{Q_2}{Q_1}$$
という式で計算できる。さらにこの熱効率は
熱\(Q\)の代わりに高温の熱源\(T_1\)と低温の熱源\(T_2\)を使って
$$\eta=1-\frac{T_2}{T_1}$$
という形に書き換えられる。導出はここではやらない。
はじめ僕は、熱\(Q\)と熱源\(T\)の違いがよくわからなかったんだけど、熱機関というものをよくイメージすることが重要みたいだ。熱源というのは石炭を燃やしてできる温度のことだから単位は\(T\)で、熱はその熱源から得られるエネルギーのことで単位が\(Q\)となっているので別物である。
もうひとつよくわからなかったのが\(T_2\)という\(2\)つ目の\(T\)方も熱源と呼ばれていることだ。こちらも僕自身よく理解していなかったのだが、ひとつの考え方は現実に温度をゼロにすることはできないので、どんな環境でもある程度温度、すなわち熱源\(T\)が存在しているということ。もうひとつはカルノーサイクルを逆向きにサイクルさせたときに低温の熱源\(T_2\)から熱\(Q_2\)を取り出す(これが冷蔵庫やクーラーが部屋を冷やしている原理だ)ので熱源という言葉の機能を果たしている、ということで僕は納得している。
この結果から動力を生み出す熱効率というのは\(2\)つの熱源の組み合わせによって決まることがわかったのだけど、これを初めて聞いたとき僕は「ああ、これが熱効率の計算の方法か」ぐらいにしか考えていなかったけど、全然大切なことを理解できていなかった。ちょっと計算してみればわかるのだけど、これの熱効率の公式の最も重要なことは、やみくもに熱源の温度\(T_1\)を上げても無駄だということを教えてくれることだ。
おそらくだけど、当時の技術者はたくさんの動力を得るためには、高い温度が必要だと考えて、高温の熱源を準備しようとしていた。しかし、例えば高熱源\(T_1\)を\(200\)℃とか高い温度にして、低熱源\(T_2\)を常温の\(25\)℃ぐらいにして\(2\)つの熱源の差を広げようというのは同じシステムの中では不可能のようだ。たぶん高熱源の影響を受けて温まってしまうのだろう。高熱源を上げれば、低熱源の方も温度が上がってしまうし、カルノーは、当時の技術者がむやみやたらに行っていた熱源の温度設定にある基準のようなものを示したことが、この熱効率の式のすごいところなのである。
例えば高熱源\(T_1\)を\(200℃(473K)\)にして低熱源を\(150℃(423K)\)だとすると
$$\eta=1-\frac{423}{473}\approx 0.11=11%$$
同じ\(50℃\)の差でも、高熱源が\(150℃(423K)\)で低熱源を\(100℃(373K)\)という組み合わせだと
$$\eta=1-\frac{373}{423}\approx 0.12=12%$$
となって、\(200℃\)と\(150℃\)の組み合わせの熱効率よりわずかながら大きくなっている。もちろんこれらの例が本当に現実に即したものかどうかは全くわからないけども、もし温度差が同じであるならば高い温度の組み合わせだからと言って、熱効率が最大になるわけではないことは理解できた。
エントロピーの概念の導入
熱\(Q\)は熱サイクルの後は、状態量ではないので同じ数値に戻ることはない。(状態量に関してはこちら)
しかし先ほどのカルノーサイクルの熱効率の式から、2つの熱源と熱の関係は
$$\frac{Q_2}{Q_1}=\frac{T_2}{T_1}$$
という式で表され、これを変形させると
$$\frac{Q_2}{T_2}-\frac{Q_1}{T_1}=0$$
となる。\(Q_2\)と\(T_2\)という低熱源側の値の組み合わせから\(Q_1\)と\(T_1\)という高熱源側の値の組み合わせを引くということは、熱サイクルの後に変化がないものと考えることができるので\(Q/T\)をひとつの状態量として考えられる。状態量というのは、変化のさせ方によらず、ある状態ならいつも同じ値を取るものである。これがエントロピーという概念の始まりである。
さっきの式をさらに一般化する。
\(Q\)がマイナスの値を取れるようにして、複数のカルノーサイクルが組み合わされているもの(実際にどういうものか僕自身イメージできていないが)とし、数字が奇数のものを高熱源側から吸収される熱、偶数のものを低熱源側に放出されるとすれば
$$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}+\frac{Q_3}{T_3}+\frac{Q_4}{T_4}+…=0$$
と表現できる。さらに\(\sum\)を使えば
$$\sum^{n}_{i=1}\frac{Q_i}{T}=0$$
経路積分を使えば
$$\oint_C \frac{dQ}{T} \,ds$$
この積分の中の分数\(\frac{dQ}{T}\)を新しい状態量としてエントロピーと名付けられるようになった。\(S\)を使って
$$dS=\frac{dQ}{T}$$
TSグラフ
これを用いて熱力学第1法則が少し書き換えられる
$$dQ=dU+PdV$$
が熱力学第1法則の式だったと思うけど、これに$$dS=\frac{dQ}{T}$$を変形した\(dQ=TdS\)を代入すると
$$TdS=dU+PdV$$
となる。
これを使ってPVグラフのカルノーサイクルをTSグラフに描き直すと長方形のサイクルで表される。
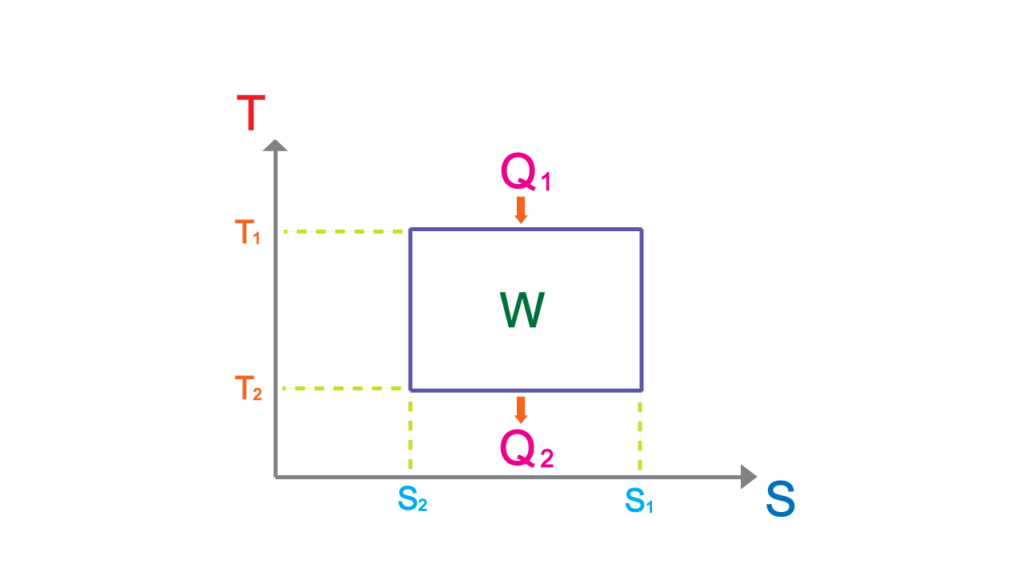
この面積が仕事\(W\)と一致する。
エントロピーは増大する
カルノーサイクルが不可逆過程の可能性も考えるとクラウジウスの不等式が導かれて、エントロピーの式に不等号を付けることができる。
$$dS\geq \frac{dQ}{T}$$
これがエントロピーが増大するという式だ。後で詳しくするが、この事実は自発的変化の指標となる。
エントロピーをイメージする
それぞれの導出は他に任せるとして(後で追記するかもしれない)、次に進もう。ここでの目的は、エントロピーが熱力学で使われる概念なのに、なぜ「乱雑さ」や「情報量」という言葉で使われるのかである。
これまでのところ、エネルギーは熱という形で温度の高いところから温度の低いところに自然に(自発的に)移動するという自然の法則から始まり、カルノーサイクルという理想的な熱サイクルをよく考察することで、\(dQ/T\)という新しい状態量を生み出すことができた。それを\(S\)を使ってエントロピーと名付けることにした。式は
$$dS=\frac{dQ}{T}$$
日本語で書くと
エントロピーの変化=与えられた熱/温度
ということになる。
わかりやすく温度の違う\(2\)つの箱の中の空気を考えてみよう。\(A\)は温度が高く、\(B\)は低い温度として、それぞれに同じ熱を加える。
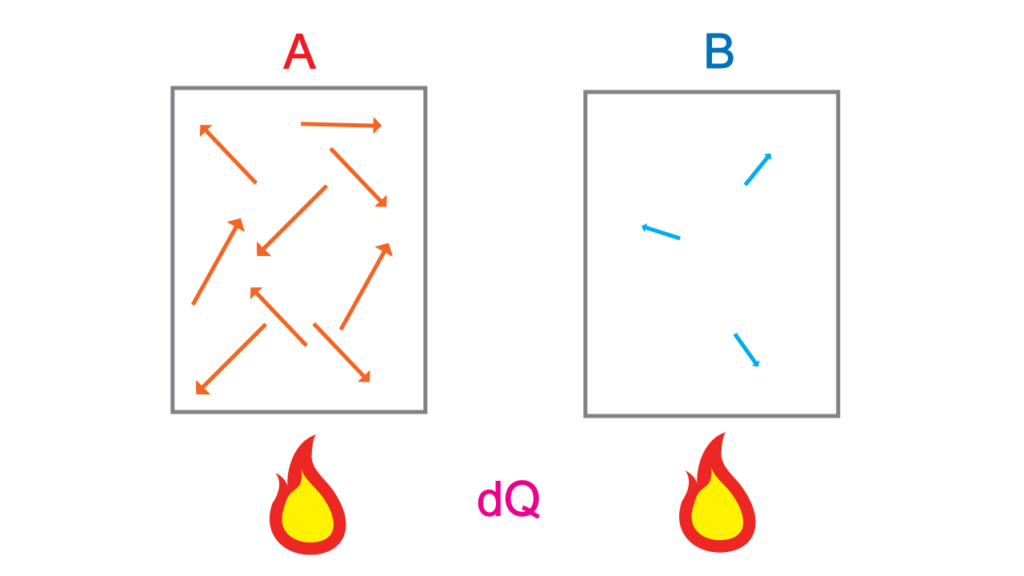
\(A\)の方は温度が高いので空気の分子が\(B\)の箱のものより激しく動き回っていることだろう。反対にBの空気分子はそこまで活発ではない。温度と分子の運動の関係は
$$\frac{1}{2}m\overline{v}^2=\frac{3}{2}kT$$
から理解できる。明らかに温度\(T\)が上がれば、速度\(v\)が大きくなるという比例の関係にある。
分子の動きが穏やかな\(B\)の方に熱を加えると、動きが活発になりやすいだろう。逆にすでに分子の動きが活発である\(A\)の方に同じだけの熱を加えてもそこまで変化はないかもしれない。
エントロピーのたとえ話
ここで、このようなたとえ話はどうだろうか。
おしゃべりをしている人の多い食堂のような場所\(A\)とみんなが静かに勉強している図書館\(B\)という場所があって、そこの誰かの携帯電話が鳴る(熱)と食堂の方ではもともと騒がしいので誰も気にも留めないけど、図書館の方ではその呼び出し音がうるさく感じられると思う。これはエントロピーの式をイメージするのにちょっとだけ良いかもしれない。
\(A\)のような、もともと騒がしい(乱雑な)ところで電話が鳴ろうとも、騒がしさ(乱雑さ)はあまり変わらない。
同じように、\(A\)の温度の高い、つまり分子の動き(乱雑さ)がもともと大きな箱を熱したとしても、分子の動き(乱雑さ)はあまり変わらない。
エントロピーが乱雑さと呼ばれる意味合いを少しだけ理解できたかな。
統計力学的エントロピー
エントロピーは別の形で表現されるのをご存じだろうか。
ボルツマンの関係式と呼ばれ
$$S=k\ln(W)$$
という形である。\(k\)はボルツマン定数\((1.38×10^{-23}[\frac{J}{K}])\)。\(W\)(Workではない)はミクロ的な状態の場合の数と呼ばれている。さっぱりハテナな訳だが、まずは導出から。
まず初めに\(V_1\)という容器の中に、\(1mol\)の分子\((n=1)\)が入っているとする。その容器の大きさを\(V_2\)に広げたときの仕事を求めるときは
$$W=\int_{V_1}^{V_2}PdV$$
で計算できる。\(P=\frac{nRT}{V}\)なので、これを代入すると
$$=\int_{V_1}^{V_2}\frac{nRT}{V}dV$$
$$=nRT\int_{V_1}^{V_2}\frac{1}{V}dV$$
積分を計算し、さらに\(n=1\)なので
$$=RT(ln{V_2}-ln{V_1})$$
$$=RTln{\frac{V_2}{V_1}}$$
今、容器の中には\(1mol\)の分子が入っているので、分子\(1\)個あたりの仕事を求めようとすると、アボガドロ定数\(N\)で割ってやればいい。
$$\frac{W}{N}=\frac{R}{N}T\ln{\frac{V_2}{V_1}}$$
\(\frac{R}{N}\)はボルツマン定数\(k\)のことなので、結局
$$\frac{W}{N}=kT\ln{\frac{V_2}{V_1}}$$
となる。
この\(V_1\)が\(V_2\)に膨張させる過程が等温変化ならば\(kT\ln{\frac{V_2}{V_1}}\)だけエネルギーを与えれば良いことになる。つまりこれだけの熱/(Q/)を与えるのと同じことである。
式で表せば
$$Q=kT\ln{\frac{V_2}{V_1}}$$
その両辺を\(T\)で割ると
$$\frac{Q}{T}=k\ln{\frac{V_2}{V_1}}$$
最後にエントロピーを\(S\)に書き直して
$$S=k\ln{\frac{V_2}{V_1}}$$
これがボルツマンの関係式の導出である。
しかしちょっと見た目が違う。どうやら\(ln\)の中が違う。\(2\)つを並べてみよう。
$$ボルツマンの関係式\ S=k\ln(W)$$
$$今導出したもの\ S=k\ln{\frac{V_2}{V_1}}$$
これらは同じもののはずである。最初に紹介したとき\(ln\)の中の\(W\)は仕事の\(W\)ではなく「状態の場合の数」という言い方をした。それが\(\frac{V_2}{V_1}\)という膨張した空間とその前の空間の大きさの割合と同じだと言っているのだ。これについてもう少し考えてみたい。
そもそも場合の数とは何か。辞書によれば「起こりうる場合の総数」ということで、サイコロなら\(6\)という数字がそれにあたる。
例えばさっきの体積の膨張を\(2\)倍にしてみよう。言い方を変えれば分子\(1\)個が入る部屋が\(2\)つになったということだ。
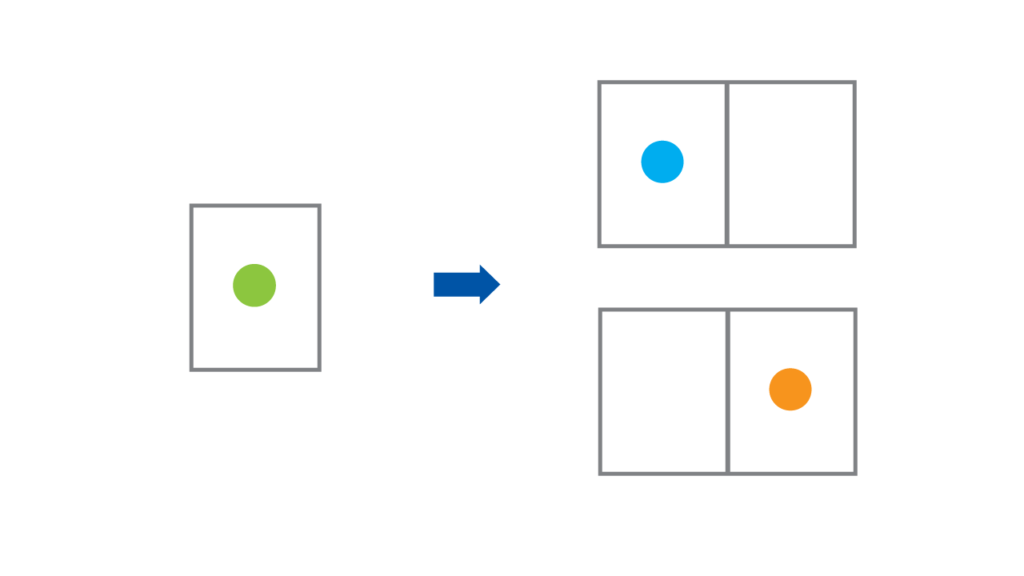
これは分子\(1\)個のとる「場合の数」を\(2\)倍にすると言えるのではないか。つまり部屋が\(1\)つしかなかった\(V_1\)の状態では、「起こりうる場合の数」は\(1\)つしかない。しかし、部屋が\(2\)つになった\(V_2\)という状態では、「起こりうる場合の数」は\(2\)通りである。
式の方でも、\(2\)倍にするということは\(2V_1=V_2\)という関係なので、これを代入すると
$$S=k\ln{\frac{2V_1}{V_1}}=k\ln{2}$$
となり、状態の場合の数\(W\)の場所に\(2\)という数字が入っており、結果と一致している。どうやら体積の増加の割合は状態の場合の数とイコールで結べるようだ。
$$積の増加の割合=状態の場合の数$$
まあこれまでは良いとして、まだエントロピーの式に\(ln\)という対数が付いているのが気持ち悪いと感じるかもしれない。それにまだエントロピーが「情報量」と呼ばれる理由はクリアでない。
こんな例はどうだろう。
見た目が全く変わりのない\(1\)個の宝石とニセモノが\(31\)個あったとし、宝石の重さはニセモノより明らかに大きいものとする。この中から天秤を使って宝石を選び出すときは、半分づつ天秤にかけ、重いほうをまた半分に分けて、また重いほうを半分に…としていけば最終的に宝石を選び出すことができる。
$$32→16→8→4→2→1$$
この方法を使えば\(5\)回の試行で終了する。初めの\(32\)個を状態の場合の数とし、\(5\)回という試行を情報量と考えれば、対数\(\log_{2}\)を使って
$$5=\log_{2} 32$$
と表すことができ
$$情報量=\log 状態の場合の数$$
という関係があることがわかる。状態の場合の数というのはニセモノの数の大きさでもあるので、それが大きくなると情報量(エントロピー)が増えるのは納得だ。
しかし、まだ対数\(log\)を使う完全な理由にはつながっていない気がするが、他に\(log\)がどのようなときに使われるか見てみよう。
人間の感覚は対数的
対数というのは、大きな数のかけ算を簡単な足し算に変換できるので、ただ計算に便利というイメージがある。
確かにそういう面もあるけど、生活の中で実用化されているものに目を向けると、対数の別の利便性が見えてくる。
対数が使われているものは、ゆれの大きさを表す「震度」、音の大きさを表す「dB(デシベル)」、星の明るさを表す「等星」やピアノの「音階」なども対数がとられている。それらは単純なエネルギーの大きさや振動数の増減は人間の感覚とマッチしていないことを示している。地震のエネルギーが\(10\)倍になったとき、人間の感じる地震の大きさは\(2\)倍になるし、音のエネルギーが\(10\)倍になると、人間の感じる音の大きさは\(2\)倍になる。
お金に関しても対数が使われることがある。例えば、\(100\)万円もらえるとなったら普通に嬉しいし、\(200\)万だったらもっと嬉しいだろう。しかし、もらえる金額が\(1\)憶とか\(10\)億円とかなってくると感覚がマヒして、\(100\)万円ぐらいの金額のありがたみはなくなってしまう。もちろん嬉しいことは嬉しいだろうけど、もらえる金額の大きさとそれを受け取った人の幸福感は完全に比例の関係ではないということだ。
ここで話を食堂と図書館に戻そう。食堂にはたくさんのお喋りしている人がいるので乱雑さはすでに大きい。そこに騒がしいグループが入室しても、ほとんど誰も気に留めない。しかし、みんなが静かに読書や勉強している図書館、つまり乱雑さの小さい場所に騒がしいグループが入っていくと騒がしさが際立つ。この絶妙な加減を対数が表してくれるのだ。
エントロピーは初め、極めてつかみどころのない無機質な示量に思われていたけど、こうしてみると人間の感覚に対応したところもあって、今ではちょっと親近感さえ覚える。なんかかわいいやつだと思った。
状態の変化の方向
ここではエントロピーが活躍する場、というか実際にどのような場面で使われるのかを見てみよう。
ある物質\(A\)が物質\(B\)に変化することがある。しかし物質\(B\)から物質\(A\)には変化する反応は起きない。多くの場合、一方通行の反応のようだ。この反応の方向を決めるものは一体何なのだろうか。
実は、エネルギーとエントロピーの大きさによって決定されるのだ。エネルギーの高い物質は不安定で、エネルギーの低い物質は安定なので、エネルギーは反応をできるだけエネルギーの低いほうへと導く。位置エネルギーの大きい高いところにある物体は、位置エネルギーのを小さくするように低い場所に向かって力が働いている(重力によって引っ張られている)。一方で、これまで見てきた通り、エントロピーは乱雑さを増加させるので、反応をエントロピーの大きいほうへ導く。反応の方向はこの\(2\)つの力の大小関係で決まることになるのだ。
化学の実験では大体低圧の状況で行われるので、エンタルピー\(H\)をエネルギーとして扱う。
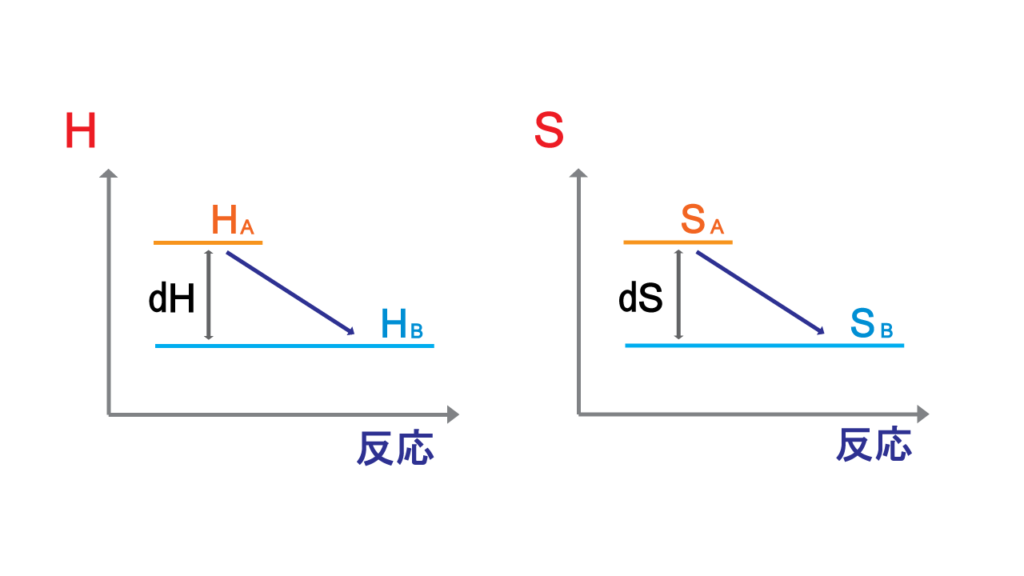
エンタルピーが減少するというのはエンタルピーとしては有利な進行だけど、エントロピー的には不利な進みである。
これを解決するために生み出されたのが「自由エネルギー」である。
まず今はエンタルピー\(H\)に注目しよう。さっきの物質\(A\)から物質\(B\)に変化する反応で高いエネルギー状態から低いエネルギー状態へ変化する。エンタルピー的には有利に進行するのだけど、その時余ったエネルギー\(dH\)が生じ、発熱反応として放出される。しかし、エントロピーは減少し不利な反応が進行している。
このエントロピーに不利な反応を進行させるように、その不利な分を補うだけのエネルギーが必要なのである。そこで、エントロピーの式\(dS=\frac{dQ}{T}\)を変形させて\(TdS=dQ\)とすると、左辺のエントロピーの次元がエネルギーになる。先ほどの放出された\(dH\)の一部をエントロピーの減少(不利な進行)を抑えるのに使われたと考えれば辻褄が合う。発見者のイニシャル\(G\)を使って
$$dG=dH-TdS$$
と表される。ギブズの自由エネルギーと呼び、\(dG<0\)のとき反応が進行することになる。




コメント