Fluid Equation

前回は、宇宙論でよく使われるフリードマン方程式をニュートン力学的に導出した。

$$ \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho -\frac{Kc^2}{a^2} $$

これは宇宙の広がりの具合を表す方程式で、なかなか難しそうなのに、意外とシンプルに導き出せたような感じがする。

今回は少し違った視点で宇宙を考えることにする。

宇宙の広がり具合をこのフリードマン方程式は表していると言ったが、その式の中には右辺第１項の重力の項と第２項の曲率の項しかない。第１項の重力の項には密度$\rho$があるが、もし宇宙全体をひとつの球体と見立てて、それが広がったり縮んだりするのなら、それに伴って中の圧力$P$だったり、他の要素も一緒に変わるはずである。

そこで宇宙がMという質量の球体だとするならば、有名なアインシュタインの式

$$E=mc^2$$

から、全体のエネルギーが算出できる。

ちなみに何気なく使っているこの式$E=mc^2$はどうやって導出されるか知っているだろうか。式自体が有名すぎて、あまりその導き方は注目されていないかもしれないけど、なかなか面白いのだ。現在ページを作成中。

ともあれ、この式に前回求めた球体の質量$M=\frac{4}{3} \pi \rho r^3 $とスケール因子を用いた球体の半径$r=ax$を代入して

$$E=\frac{4}{3}\pi c \rho a^3 x^3$$

さらに、スケール因子の式$r=ax$において、$x$は$Comoving\ Coordinate$ということだったが、これはいわば宇宙の拡大縮小に伴って変わる基盤のメモリやマス目のようなものなので、これを１という単位距離にしてやってもよい。その１メモリ分を１という単位にしようということだけのことだ。例えば普通のモノサシで測った距離が３ｃｍだとしたら、３×１メモリ分（１ｃｍ）ということだけども、わざわざ１メモリが２ｃｍとか３ｃｍとか半端な数にはしない。１メモリは１という何かしらの単位距離であるべきなのだ。

そうすると

$$E=\frac{4}{3} c \pi\rho a^3$$

になる。厳密にいえばスケール因子と実際の距離というのは違うものだけど、ほぼほぼ同じものとして扱っていくことに慣れていってもらいたい。まだ慣れていないという人は、まあ「郷に入っては郷に従え」ということで、そういうもんだと、まず受け入れてしまうのも何かを学び始めるときのひとつのコツかもしれない。小さいことに引っかかって、前に進めないことの方が非効率である。

それから$E=\frac{4}{3} c \pi\rho a^3 $の中の密度$\rho$とスケール因子$a$は共に時間に依存しているので、Eを時間微分すると

$$\frac{dE}{dt}=\frac{4}{3}\pi c^2 \bigg(3a^2 \rho \frac{da}{dt} + a^3 \frac{d\rho}{dt}\bigg)$$

となる。

さらに宇宙の体積は時間とともに変化しているので、スケール因子$a$で表した体積$V=\frac{4}{3}\pi a^3$も時間で微分してみる。今回は時間に依存しているのはスケール因子$a$だけなので簡単。

$$\frac{dV}{dt}=\frac{4}{3}\pi \bigg(3a^2 \frac{da}{dt}\bigg)=4\pi a^2 \frac{da}{dt}$$

エネルギーが変わったり、密度と圧力の関係を取り扱うということで、ここで熱力学の考え方を使おう。

まずは熱力学第一法則とはどのようなものだったか

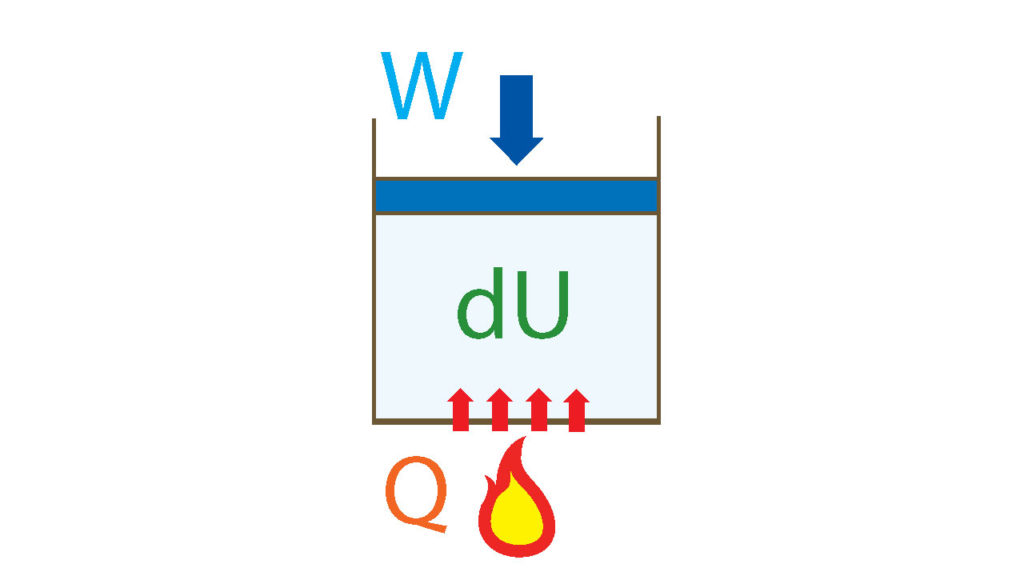
$$dU=Q-W$$

である。熱力学第一法則には２種類の表記方法がある。それは$dU=Q-W$と$dU=Q+W$だけれども、外からの仕事がそのモノに何かしら影響を与える場合は後者の式を使う。（念のため付け加えておくけども、今から述べるその後者の方（$W$の符号がマイナス）は宇宙論で使わない方である。なぜなら宇宙の外側から影響は考えないからだ。）

$$dU=Q+W$$

これは、熱$Q$と外からの仕事$W$が気体のエネルギー（内部エネルギー）$dU$をどう変化させるのか、という視点に基づいている。

しかし、今回は宇宙全体が球体と仮定しているわけだから、その外側からの温度変化や仕事があるとは普通考えない。（宇宙の外側のことを考えるのはおもしろいと思うんですけどね。みなさんは神様とかいるとか考えますか？）

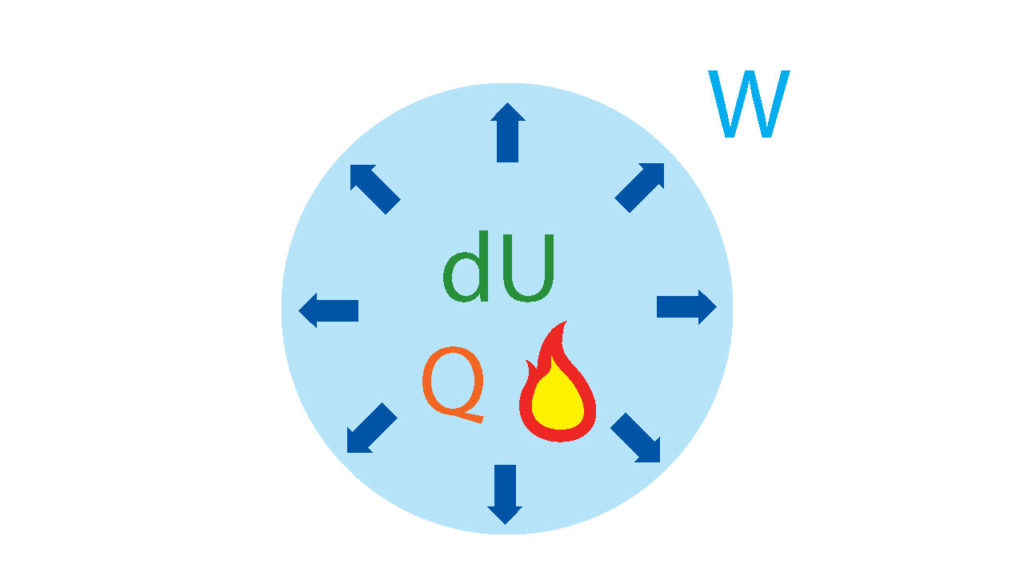
その代わりに、宇宙の球体の内側のエネルギーが変化して、球体の殻を内側から押す圧力が生まれると考える。熱力学第一法則の仕事Wの符号が変化するのはこのためだ。

この場合（この宇宙を考えた場合）

$$ dU=Q-W $$

となる。もともと$Q$を主役にした

$$ Q=dU+W $$

という形であったので、こちらで覚えた方がわかりやすいかもしれない。違うのは$W$の符号だけだ。

$E$も$U$もどちらもエネルギーを表しているので、$dU=dE$としても問題はない。

熱力学をかじったことのある人なら、$W=PdV$というのはよくご存じだろうし、エントロピーの式から$Q=TdS$とできる。

さらに、話をシンプルにするために$ds=0$とする。アカデミックな用語を使えば、エントロピー$S$が変化しないということで、可逆的な過程を想定しているという意味になる。

これはどういう意味だろうか、「宇宙が膨らんだり縮んだりしても元の状態に戻ることができる」ということだろうか。いずれにせよ、$dS=0$と置くことで$Q=0$になるので、式は簡単になった。シンプルな状況から考えていくのが、科学の常套手段だ。

結局、式自体は

$$dE+PdV=0$$

となる。これに先ほど計算した$\frac{dE}{dt}=\frac{4}{3}\pi c^2 (3a^2 \rho \frac{da}{dt} + a^3 \frac{d\rho}{dt}) $と$\frac{dV}{dt}=\frac{4}{3}\pi (3a^2 \frac{da}{dt})=4\pi a^2 \frac{da}{dt}$を使って、式に代入しよう。

$$\frac{4}{3}\pi c^2 \bigg(3a^2 \rho \frac{da}{dt} + a^3 \frac{d\rho}{dt}\bigg)+\frac{dV}{dt}=\frac{4}{3}\pi \bigg(3a^2 \frac{da}{dt}\bigg)=4\pi a^2 \frac{da}{dt}=0$$

これの両辺に$\frac{3}{ac^2}$をかけてやり、時間微分をドット$・$で表してあげれば

$$\dot{\rho}+3\frac{\dot{a}}{a}\bigg(\rho + \frac{P}{c^2}\bigg)=0$$

これがFluid Equationと呼ばれているものだ。日本語で何と呼ぶかは知らない。

とくに面白いことのない結果かもしれないが、これはフリードマン方程式とは違って、宇宙の大きさと内側から押す圧力の関係がみえるようになる。これも後々よく使われることになる。

わかってもらいたいのは、宇宙の勉強で使われるような式が基本的な物理の方程式から導き出されるという点だ。