
フリードマン方程式の意味
宇宙を勉強するっていったって、いったいどうすればいいんだろう。
望遠鏡覗けばいいのか?それとも特殊な機械が必要なのだろうか?
最先端の研究や観測のためには、そういったものの力を頼らなければいけないかもしれない。もっと概念的なものを知りたい。宇宙の研究者たちはどんな考え方をしているのか。どんな数式を使っているのかに興味がある。
宇宙論(Cosmology)について調べていると、まずフリードマン方程式というものに出くわす。天下り式になってしまうが、とりあえずどんな方程式なのか見てみよう。
$$ \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho -\frac{Kc^2}{a^2} $$
これは宇宙の膨張の度合いを表す式だ。
左辺には\(\dot{a}\)を\(a\)で割って2乗したものがある。\(a\)というのはスケール因子と呼ばれていて、 宇宙の大きさを表しているという認識で今は問題ないと思う。それに・が上に付いて\(\dot{a}\)になっている。これは時間で微分したものだから丁寧に書くと
$$\dot{a} = \frac{da}{dt}$$
となっている。2乗してあるのは放っておいて、宇宙の大きさを表すスケール因子\(a\)が時間で微分されているとはどういうことだろう。
物理では、速度\(v\)は位置を表す\(x\)の時間微分であった。
$$v = \frac{dx}{dt}$$
それと同じ感じで、大きさを表すスケール因子\(a\)の時間微分\(\dot{a}\) は宇宙の広がる速度的なものと言って差し支えないはず。
それに\(a\)が分母に付いていたり、2乗されたりしているが、本質的な式の意味は変わらないはずだ。
右辺を見てみよう。
最初の項は、万有引力定数\(G\)と物質の密度\(\rho\)がある。これらは物質の重力による効果だ。
第2項では、空間の曲率\(K\)があり、その効果を示す項になっている。ここでは説明しない、というかこれを書いている時点では、僕自身上手く説明する自信はないのだけど、相対性理論というのは、重力を空間のゆがみで捉えようという試みであると言われている。だから、曲率\(K\)という概念はとても重要なのだ。
フリードマン方程式の導出(古典的)
今回の趣旨は、このフリードマン方程式がどのように導出されるのか、であった。
方法としては、相対性理論から導き出されるものもあるが、今回はニュートン力学から導出する方法をやってみよう。こっちの方が簡単だ。
まずは宇宙を大きな球体と仮定して話を進める。
その球体は均一に質量があると考え、トータルの質量を\(M\)、その球体の表面に位置する小さな点を質量を\(m\)、球体の中心からその点までの距離を\(r\)とする。

それらの間に生じる重力は、万有引力の方程式から
$$F= G \frac{M m}{r^2}$$
そして、球体の質量\(M\)を密度\(\rho\)と体積\(V=\frac{4 \pi r^3}{3}\)で表し、\(M=\rho V\)から
$$M=\frac{4 \pi \rho r^3}{3}$$
これを\(F= G \frac{M m}{r^2}\)を代入して
$$F=\frac{4 \pi G \rho r m}{3}$$
万有引力による位置エネルギーは
$$U=-\frac{G M m}{r}$$
なので、同じように\(M=\frac{4 \pi \rho r^3}{3}\)を代入して
$$U=-\frac{4 \pi G \rho r^2 m}{3}$$
とできる。
さらに、エネルギー保存の法則から
$$E=K+U$$
\(K\)は力学的エネルギーなので、\(\frac{1}{2}mv^2\)だけど、ここでは先ほどの\(r\)の微分したもの\(\dot{r}\)を使って、\(\frac{1}{2}m\dot{r}^2\)とする。
位置エネルギーは、さっき計算した\(U=-\frac{4 \pi G \rho r^2 m}{3}\)を使って
$$E=\frac{1}{2}m\dot{r}^2-\frac{4 \pi G \rho r^2 m}{3}$$
さて、宇宙は広がっている、もしくは縮小していると考えているわけだけども、そうなると球体の中心からの距離\(r\)は時間とともに変化していることになる。そこで、記事のはじめに紹介した、スケール因子\(a(t)\)を導入する。\((t)\)と書かれているのは、そのスケール因子は時間の関数、つまり時間とともに変化する値であることを表している。
さらに、\(Comoving\ coodinate\ x\)も用いる。これは実際の距離ではなく、拡大縮小している座標自身というか、目盛りの数という認識で問題ないはずだ。
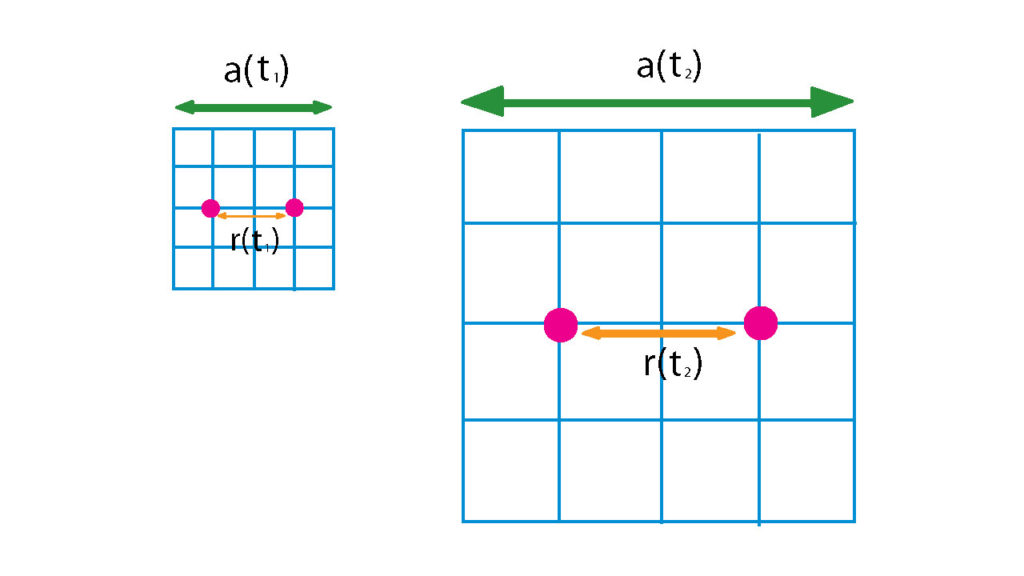
これらを組み合わせて
$$\vec{r}=a(t)\vec{x}$$
とすると、時間変化に合わせて長さの変わる距離\(r\)を表すことができた。
さっきのエネルギー保存の法則の式の中にスケール因子\(a\)を取り入れたい。ちなみに、\(r\)の時間微分は\(\dot{r}=\dot{a}x\)なので
$$E=\frac{1}{2}m(\dot{a}x)^2-\frac{4 \pi G \rho (ax)^2 m}{3}$$
ここから両辺に\(\frac{2}{m a^2 x^2}\)をかけて、さらに\(-\frac{2 U}{m x^2}=kc^2\)と置くと
$$ \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho -\frac{kc^2}{a^2} $$
となる。相対性理論的な導出をすれば、この式の意味をより深く理解できるかもしれないが、最初のとっかかりとしては悪くないと思う。宇宙を研究している人たちはこの式を元に、いろいろこねくり回してやっているようだ。
さあ、始まりますよ。



コメント